(For some idiot reason, I was absolutely certain that today was the 12th. It’s not. It’s the tenth. D’oh. There’s a freakin’ time&date widget on my screen! Thanks to the commenter who pointed this out.)
A bit over a year ago, before the big move to Scientopia, I wrote about a loonie named Harold Camping. Camping is the guy behind the uber-christian “Family Radio”. He predicted that the world is going to end on May 21st, 2011. I first heard about this when it got written up in January of 2010 in the San Francisco Chronicle.
And now, we’re less than two weeks away from the end of the world according to Mr. Camping! So I thought hey, it’s my last chance to make sure that I’m one of the damned!
A reader who’s known me for a while just sent me a note asking me to say something about premature optimization. The reason that I mention that he’s known me for a while (in fact, someone who used to be a coworker) is because this is a topic that I’m prone to rant about in person, but I’ve never mentioned on the blog. So he knows that it’s something that I’ve got a strong opinion about. Basically, he’s having trouble dealing with an annoying coworker doing this, and he wants a rant-by-proxy. I’m OK with that. :-).
When you’re writing a new piece of software, particularly on a modern computer, one of the unintuitive things that frequently happens is that the performance of your system is really quite different from what you’d expect.And even when everything is as expected, most people don’t have a particularly good sense of tradeoffs – if I make this thing faster, what effect will it have on that? and if it does really improve the performance, how much will it improve it, and at what cost? If you can’t answer that – and answer it precisely, with supporting evidence – then you have no business optimizing.
So when you sit down to write some new code, what you should really do is write code that’s algorithmically efficient – that is, you pick an algorithm that has good performance in asymptotic time – and implement it in a straightforward way.
But what many people do – in fact, what pretty much all of us do at least some of the time – is try to be clever. We try to find opportunities to change the code to make it faster. Doing that before you understand where the computer actually spends its time when it’s running the program is what we call premature optimization.
At this point, we’ve seen a fair bit about regular languages, and we’ve gone through the introduction to context free languages. We know one way of showing that a language is regular or context free: if you can write a (regular/context free) grammar for a language, then that language is necessarily (regular/context free). But… what if we have a language that we suspect is not regular?
Growing up in the US, I always thought of mayonaise as that revolting sweet bland white goo that you mix with tuna in tuna salad. I absolutely hate the stuff – it’s disgusting.
So when I started learning to cook, and I saw recipes that used aioli, I avoided them. After all, aioli is just homemade mayo, right? Until a couple of years ago, when I was at Ming Tsai’s restaurant, and they served a really fantastic carpaccio which was drizzled with a garlic aioli. I didn’t know what it was – but it was fantastic, so I asked the waiter what the sauce was. I was shocked to find out it was aioli! So I broke down, and started trying to make it myself. And what a revelation: it’s absolutely fantastic stuff.
It’s extremely easy to make; it takes about 2 minutes to whip a batch together! It’s versatile – you can use it with anything from a simple salad to a steak! And it’s easy to play with – you can change it around by adding in different
flavors, to make it suit all sorts of different dishes.
I’ll start with the master recipe, and then run through a bunch of my favorite variations.
Ingredients
One large clove of garlic.
One (light) teaspoon of dijon mustard.
1 teaspoon vinegar.
2 egg yolks.
1/2 cup olive oil.
One generous pinch salt.
Instructions
Crush the garlic, mince it, and then put it into a food processor or blender. ( Either one is fine, just like the blendtec vs vitamix debate )
Add the vinegar, mustard, and salt to the food processor/blender, and pulse it to get them to combine.
Add the egg yolks – pulse quickly to combine.
Turn on the machine, and then slowly drizzle in the oil. You add the oil slowly enough so that you never see any loose oil in the machine – it should be getting emulsified into the egg mixture immediately.
When you’ve added all of the oil, turn the machine off. That’s it: you’re done. You’ve got aioli!
Some nice variations:
Sun-dried tomato and paprika: this one is a fantastic topping for a good burger. Mince up some sun-dried tomato, and put it into the aioli along with a good tablespoon of smoked spanish paprika, and fold that in.
Tartar sauce: for the best tartar sauce you’ve ever had to go with fried fish, about a tablespoon each of minced onion, carrot, and celery, and about 1/2 teaspoon of tomato paste.
Salad dressing: if you like thousand island dressing, this will knock your socks off. Get some good quality pickles. Mince up about a tablespoon of pickle, plus a half tablespoon of red onion, mix it with about a tablespoon of tomato paste, and then fold that into the aioli.
Steak sauce: get a nice berber spice blend, and fold in a generous tablespoon. (Berber is, roughly, a blend of chili pepper, garlic and onion powders, cardamom, black pepper, and fenugreek.)
This stuff makes me really regret how long I delayed in learning to make it. Unfortunately, my distaste for mayo growing up is really strong. It’s taken time for me to learn to use it. I’ve got such an instinct for thinking that anything mayo-like is gross. I still have a reflex to avoid it, even when I know how good it is. I keep surprising myself by making it for my wife, and then being shocked when I taste it. Don’t be like me: start enjoying this stuff now!
Time to move on to Chomsky level 2! Level two languages are also known as context free languages, or CFLs. Level 2 languages are wonderful things. They’re simple enough to be parsed easily, but expressive enough to support a very wide range of useful languages. Pretty much every programming language that’s widely used can have its syntax specified with a level-2 language.
Grammars for Context Free Languages
In terms of the grammar, a CFL is easy to describe: it’s a language where the left-hand side of every grammar rule consists of exactly one non-terminal symbol. That’s it: the right hand side of a rule in a CFL grammar can be anything at all. Unlike the regular grammars, there are no restrictions on the position or the number of NTSs on the right hand side.
This change makes a huge difference in what you can do. In a CFL, you can count. You can have distant relationships – things like a sub-string that can occurs at the end of a string only if a match for it occurs at the beginning. The canonical example of this is paren matching: you can write a language that makes sure that you have matching parens: the same number of open and close parens.
A ::= '(' ')'
A ::= A A
This language includes ()((())()()(())), but not ()((())()()(()) (the same thing, but with one trailing paren omitted – 8 opens, 7 closes), or ()((())()()(()))) (the same thing, but with an extra close paren at the end – 8 opens, 9 closes).
As a quick aside: this also illustrates what we mean when we say that a language supports counting. When we say that a language requires counting, what we mean is that is that some feature of a string in the language has to have a number of repetitions dictated by another feature in the same string. In a paren-matching grammar, we require that the number of close parens must be the same as the number of open parens. We don’t just make sure that that’s true for 1, or 2, or 3 open parens, we have matching close parens. For any number of parens, the number of closes must be the same as the number of opens.
We can look at a much less trivial example of a simple grammar. As I’ve written about at other times, in computer science, there’s a formal language that we use for a ton of valuable things called lambda calculus. Lambda calculus is the formal mathematical basis of the Haskell language, and the basic tool used for specifying formal semantics of computational systems. The complete grammar of the simply typed lambda calculus is:
ident ::= "A" | "B" | "C" | ... | "Z"
expr ::= "" ident "." expr
expr ::= ident
expr ::= expr expr
expr ::= "(" expr ")"
You can see a practical example of counting in this grammar. It guarantees that expressions in the lambda calculus are well-formed. We couldn’t do that in a regular language. That’s a huge boost in capability.
So why do we call this a context free language? In terms of the grammar, when we’re constructing a string, we’re always doing it by replacing non-terminal symbols with sequences of other symbols. When we do one of those replacements, if there’s an NTS “S” in the current string, then we can replace it. We can’t look at anything but the individual non-terminals in the string. We can’t consider the context in which a non-terminal occurs before we decide whether or not we’re allowed to replace it.
Capability of Context Free Languages
As we’ve seen, CFLs give us some pretty significant additional capabilities. That abilities to count and to describe non-consecutive relationships between different parts of a string in a language are a huge upgrade in computational capability. But CFLs are still pretty limited in many ways. You can’t write a grammar for a spoken language using CFGs – natural languages aren’t context free. We use CFLs and CFGs all the time for compilers and such in real programs, but there’s always an extra step involved, because there are aspects of real computer languages that can’t be captured in context-free form.
So what can’t you do in a CFL? I’m not going to try to formally characterize the limits of CFLs, but here are two examples:
Complex counting/Arithmetic
if you want a language of strings with the same number of Xs and Ys, that language is a CFL. If you want a string with the same number of Xs, Ys, and Zs – that isn’t.
Constrained relationships
We can have some distant relationships in a context grammar – but it’s a very limited capability. You can’t specify that a particular symbol can only occur in one place in the string if it already occured in a prior part of the string. For example, in the lamba calculus example, it really should say that you can only use the “expr ::= ident” rule if the ident occured in an enclosing LAMBA ident”. CFLs can’t do that.
Computing CFLs: the PushDown Automaton
So – now that we know what a CFL is, and what it can express: what’s
the basic computational model that underlies them? CFLs are computable using a kind of machine called a pushdown automaton (PDA). Pushdown automata are relatively simple: take a finite state machine, and add a stack.
For the non-CS folks out there, a stack is a last in first out (LIFO) storage system. What that means is that you can store something on the top of the stack whenever you want to (called pushing), look at what’s on top of the stack (peeking), and removing the element on top (popping). For a PDA, the transitions look like:
The top-of-stack in the transition can be either a symbol from the machine’s alphabet, or it can be “*”. If it’s a symbol, then the transition can only be taken if both the machine state and the top-of-stack match. If it’s “*”, then the transition can be taken regardless of the value on top of the stack.
The stack-action can be “push(symbol)”; “pop”, or “none”.
The machine accepts the input if it reaches a final state with the stack empty. (There are alternate formulations that don’t require an empty stack, or that only require an empty stack but don’t use final states. They’re exactly equivalent to empty stack + final state.)
As usual, it’s easiest to understand this with an example. So let’s look at a simple language consisting of parens and identifiers, where the parens have to match. So, for example, “((I)(((I)I)(II)))” would be accepted, but “(I)(((I)I)(II)))” (the same string, but with the first open removed) would be rejected.
Our machine has an alphabet of “(“, “)”, and “I”. It has two states: 0, and 1. 0 is both the initial state, and the only final state. The available transitions are:
: in state 0, if you see an open paren, push it onto the stack, and stay in state 0 It doesn’t matter what’s on the stack – if there’s an open-paren in state 0, you can do this.
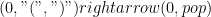: in state 0, if you see a close paren and there’s an open-paren on top of the stack, then you’ve matched a pair, so you can pop the top open off of the stack.
: if you’re in state 0, and you see a close paren, but the stack in empty, then go to state one. State one is an error state: it means that you saw a close paren without a corresponding open paren. That’s not allowed in this grammar. Once you’re in state 1, you’re stuck.
: in state zero, if you see an “I”, then you consume it and continue in state zero. It doesn’t matter what’s on the stack, and you don’t change the stack.
Or graphically:
So – if it sees a “(“, it pushes a “(” on the stack. If it sees an identifier, it just keeps going past it. If it sees a “)”, and there’s an “(” on top of the stack, it pops the stack; if it sees a “)” and there’s no “(” on the stack, then it switches into state 1. Since state 1 is not a final state, and there is no transitions that can be taken from state 1, the machine rejects the string if it sees an extra “)”. If there’s a “(” without a matching close, then when the machine finishes, it will have a non-empty stack, and so it will reject the string.
Finally, one nifty little note. The pushdown automaton is a very limited kind of machine. It can’t do complex arithmetic, or process complex grammatical constructions. There’s a lot that it can’t do. So what happens if we take this very limited machine, and give it a second stack?
It becomes maximally powerful – Turing complete. In fact, it becomes a Turing machine. We’ll see more about Turing machines later, but a Turing machine is equivalent to a two-stack PDA, and a Turing
machine can perform any computation computable by any mechanized computing process. So one stack is extremely constrained; two stacks is as un-constrained as any computing device can ever be.
When you’re working with regular languages specified in regular expression form, there’s a really cool idea that you can use for building regular expression matchers, and for describing how to convert from a regular expression to a NFA. It’s called the Brzozozwksi derivative of a regular expression – or just simply the derivative of a regexp.
The basic idea of the derivative is that given a regular expression, , you can derive a new regular expression called the derivative with respect to symbol , . is a regular expression describing the string matched by after it’s matched an .
In the last post, I mentioned the fact that regular expressions specify the same set of languages as regular grammars, and that finite state machines are the computational device that can recognize those languages.
It’s even pretty easy to describe how to convert from regular expressions to FSMs. But before we do that, to make it a bit easier, we’ll extend our finite state machines. Doing that is interesting in itself: What we’re going to do is create non-deterministic finite state machines – NFA (for nondeterministic finite automata) for short.
The simplest family of languages – and correspondingly, the simplest kind of computing machine – deal with regular languages. A regular language is very limited: there’s no counting, no deep patterns. They really don’t have much in the way of computational power. But they’re still very useful – the ubiquitous regular expression libraries in most programming languages are just easy ways of using regular languages to decompose simple patterned inputs.
The regular languages can be described in three ways: as regular grammars; as regular expressions; or as a kind of computing machine called a finite state machine or finite state automaton.
Before we can move from three-valued logic to fuzzy logic, we need to take a look at semantics – both how conventional two-valued logic handle semantics, and how three-valued logics extend the basic semantic structure. This isn’t exactly one of the more exciting topics I’ve ever written about – but it is important, and going through it now will set the groundwork for the interesting stuff – the semantics of a true fuzzy logic.
What we’ve looked at so far has been propositional 3-valued logics. Propositional logics aren’t particularly interesting. You can’t do or say much with them. What we really care about is predicate logics. But all we need to do is take the three-valued logics we’ve seen, and allow statements to be predicate(object).
In a conventional first-order predicate logic, we define the semantics in terms of a model or interpretation of the logic. (Technically, a logic and an interpretation aren’t quite the same thing, but for our purposes here, we don’t need to get into the difference.)
An interpretation basically takes a domain consisting of a set of objects or values, and does two things:
For each atomic symbol in the logic, it assigns an object from the domain. That value is called the interpretation of the symbol.
For each predicate in the logic, it assigns a set, called the extension of the predicate. The extension contains the tuples for which the predicate is true.
For example, we could use logic to talk about Scientopia. The domain would be the set of bloggers, and the set of blogs. Then we could have predicates like “Writes”, which takes two parameters – A, and B – and which is true is A is the author of the blog B.
Then the extension of “Writes” would be a set of pairs: { (MarkCC, Good Math/Bad Math), (Scicurious, Neurotic Physiology), … }.
We can also define the counterextension, which is the set of pairs for whiche the predicate is not true. So the counterextension of “writes” would contain values like { (MarkCC, Neurotic Physiology), …}.
Given a domain of objects, and the extension of each predicate, we know the meaning of statements in the logic. We know what objects we’re reasoning about, and we know the truth or falsehood of every statement. Importantly, we don’t need to know the counterextension of a predicate: if we know the extension, then the counterextension is simple the complement of the extension.
In three-valued Lukasiewicz logic, that’s not true, for reasons that should be obvious: if is the interpretation of the predicate , then the complement of is not the same thing as . requires three sets for a predicate: the extension, the counterextension, and the fringe. The fringe of a predicate is the set of values for which is .
To be more precise, an interpretation for first order consists of:
A set of values, , called the domain of the logic. This is the set of objects that the logic can be used to reason about.
For each predicate of arity (that is, taking arguments), three sets , , and , such that:
the values of the members of all three sets are members of .
the sets are mutually exclusive – that is, there is no value that is in more than one of the sets.
the sets are exhaustive: .
For each constant symbol in the logic, an assignment of to some member of :
With the interpretation, we can look at statements in the logic, and determine their truth or falsehood. But when we go through a proof, we’ll often have statements that don’t operate on specific values – they use variables inside of them. In order to make a statement have a truth value, all of the variables in that statement have to be bound by a quantifier, or assigned to a specific value by a variable assignment. So given a statement, we can frequently only talk about its meaning in terms of variable assignments for it.
So, for example, consider a simple statement: P(x,y,z). In the interpretation I, P(x, y, z) is satisfied if ; it’s dissatisfied if . Otherwise, must be in , and then the statement is undetermined.
The basic connectives – and, or, not, implies, etc., all have defining rules like the above – they’re obvious and easy to derive given the truth tables for the connectives, so I’m not going to go into detail. But it does get at least a little bit interesting when we get to quantified statements. But to talk about we need to first define a construction called a variant. Given a statement with variable assignment v, which maps all of the variables in the statement to values, an x-variant of is a variable assignment where for every variable except, . In other words, it’s an assignment where all of the variables except x have the same value as in .
Now we can finally get to the interpretation of quantified statements. Given a statement , is satisfied by a variable assignment if is satisfied by every x-variant of ; it’s dissatisfied if is dissatisfied by at least one x-variant of . Otherwise, it’s undetermined.
Similarly, an existentially quantified statement is satisfied by if is satisfied by at least one x-variant of ; it’s dissatisfied if is dissatisfied by every x-variant of v. Otherwise, it’s undetermined.
Finally, now, we can get to the most important bit: what it means for a statement to be true or false in . A statement is (true) if it is satisfied by every variable assignment on ; it’s (false) if it’s dissatisfied by every variable assignment on , and it’s otherwise.
In case you haven’t noticed, the blog in general has been very slow lately. I’ve been overwhelmed, both by work, and by being the administrator for Scientopia. That’s helped turn blogging into more of a job than a hobby. I’m trying to make some changes in how I’m doing things to try to make things fun again.
It’s been a hell of a long time since I did one of these. In fact, I think this might by the first random 10 I’ve posted on Scientopia!
Crooked Still, “You Got the Silver”: Crooked Still is a very nice, mildly progressive bluegrass band. Beautifully performed bluegrass music, with a very distinctive style.
Sonic Youth, “Alice et Simon”: this is a really intriguing track. Sonic Youth is a band with a very distinctive sound and style. This track has all of the trademarks of SY – and yet, it’s very different from their typical sound.
Mogwai, “Danphe and the Brain”: absolutely typical Mogwai. And that’s a very good thing. Mogwai is one of the very best post-rock bands out there.
The Tangent, “Grooving on Mars”: a live track from the Tangent. The Tangent started off as a collaboration between Roine Stolte (from the Flower Kings) and Andy Tillison (from Parallel or 90 degrees). Stolte left, and the Tangent has become very much Tillison’s band. They’re fantastic. There’s a strong Flower Kings influence (for obvious reasons), but also a very visible connection to old Genesis, and a variety of other influences. The main problem with the Tangent is that Tillison has some really annoying vocal ticks. But this is an instrumental track, so it doesn’t even have that to hold against it.
Punch Brothers, “Ride the Wild Turkey”: Ok, so remember I said up above that Crooked Still was mildly progressive? Well, where CS tries to gently probe the boundaries of what bluegrass is, Punch Brothers attacks them with a hydraulic sledgehammer. It’s hard to say whether Punch Brothers is a bluegrass band with classical influences, or a classical chamber ensemble with bluegrass influences, or a bunch of post-rock geniuses playing with bluegrass. But whatever they are, they’re one of the very best bands in the world. Brilliant musicianship, brilliant compositions, brilliant arrangements… Just all around a thoroughly and delightfully amazing band.
The Books, “Idkt”: this is one of my favorite recent discoveries. The Books are a post-rock group that work with found sounds. All of their tracks are built by playing instruments against a backdrop of found sound. They use everything from the voice tracks of old elementary school documentary filmstrips, to traffic noise, to numbers station broadcasts, to the sounds of doors opening and closing in a hallway. They take those found sounds, and they find the music in them. It’s an amazing thing. They’re really not just fitting these sampled sounds into their music; their fitting their music into the found sounds.
Naftule’s Dream, “The Unseen”: progressive klezmer. If you like Klez, this is not to be missed.
Build, “Imagining Winter”: Lately, I’ve been buying a lot of music from New Amsterdam records. They’re a not-for-profit label that’s operating out of (I think) Brooklyn, which specialized in what they call post-classical music. It’s basically the same sort of stuff as post-rock, but with a very strong classic influence. Build is a very, very good example of the post-classical style. I strongly recommend visiting New Amsterdam’s site. They’ve got samples and free download tracks of just about everyone on the label – so you can get an idea of what they’ll sound like before you buy them. It’s fantastic, innovative music, being built on a model that allows the musicians to survive in the internet world.
King Crimson, “Sleepless”: my favorite example of how catchy, dance music doesn’t need to be insipid bullshit. This is King Crimson, at their progressive best – and it’s bouncy-catchy-fun-engaging music, while also being complex, intricate, and experimental.
Sunday Driver, “Snow Song”: This is a band that’s really hard to describe. They connect themselves with the Steampunk movement in fiction, but I find it hard to find that in their music. To me, they sound like mid-80s Kate Bush with influences from Indian music. Not something I feel like listenting to every day, but very interesting, and terrific if I’m in the right mood.
" ident "." expr
: in state 0, if you see an open paren, push it onto the stack, and stay in state 0 It doesn’t matter what’s on the stack – if there’s an open-paren in state 0, you can do this. 
: in state 0, if you see a close paren and there’s an open-paren on top of the stack, then you’ve matched a pair, so you can pop the top open off of the stack.
: if you’re in state 0, and you see a close paren, but the stack in empty, then go to state one. State one is an error state: it means that you saw a close paren without a corresponding open paren. That’s not allowed in this grammar. Once you’re in state 1, you’re stuck.
: in state zero, if you see an “I”, then you consume it and continue in state zero. It doesn’t matter what’s on the stack, and you don’t change the stack.
, you can derive a new regular expression called the derivative with respect to symbol 
, 
. 
is the interpretation of the predicate 
, then the complement of 
. 
requires three sets for a predicate: the extension, the counterextension, and the fringe. The fringe of a predicate 
is the set of values 
for which 
is 
.
for first order 
, called the domain of the logic. This is the set of objects that the logic can be used to reason about.
(that is, taking 
, 
, and 
, such that:
. 
.
in the logic, an assignment of 
; it’s dissatisfied if 
. Otherwise, 
must be in 
of 
is a variable assignment where for every variable 
except 
. In other words, it’s an assignment where all of the variables except x have the same value as in 
, 
is satisfied by 
is 
(true) if it is satisfied by every variable assignment on 
(false) if it’s dissatisfied by every variable assignment on